Analyzing Theoretical and Practical Implementations of Set Algorithms: Part 1
Here, I implemented two different set algorithms in Python, sorted list and unsorted list. I also compared their performances for inserting and searching a value in a set. The link to my code on GitHub is here. This is the first part of 2-part series. In the next blog entry, I will write about balanced and unbalanced trees, and their performances.
Algorithms
The two algorithms I compared are sorted list and unsorted list. These are the steps I took for my project:
With a set algorithm, for each n = 25, 29, 213, and 217:
1. Create a set S1, and time the following:
a. Insert each even number in range(0, n) in order into a set S1.
b. Check whether S1 contains each value in range(0, n).
2. Create a list of n random numbers, and a new set S2. Time the following:
a. Insert the first n/2 random numbers into S2.
b. Check whether S2 contains each random number.
In summary, I tested insertion and containment check for n sizes of 24, 28, 212, and 216, in incremental and random orders.
Sorted List Set
When a SortedListSet is initialized, it creates an empty list:
class SortedListSet(object):
def __init__(self):
self.values = []For sorting, I used binary search algorithm for finding the index of the value when inserting and checking containment. The binary search algorithm returns the index of the value:
def binary_search(self, value, l, start, end):
middle = (start + end)/2
# If this l is empty, 'start'
# and 'end' will be the same.
if end == start:
return middle
elif l[middle] == value:
return middle
# We don't need to consider middle anymore
# because we ruled it out above.
# So we recurse with middle +/- 1.
# Here, we go with middle + 1.
elif l[middle] < value:
return self.binary_search(value, l, middle + 1, end)
elif l[middle] > value:
return self.binary_search(value, l, start, middle)
insert inserts the value at the correct index that
binary_search returned, with Python's built-in function,
insert. Contains check returns True or False depending on
whether the value at the index matches the queuried number:
def insert(self, value):
index = self.binary_search(value, self.values, 0, len(self.values))
# Index cannot be larger than the len(self.values)
if index == len(self.values) or value != self.values[index]:
# Use Python's built-in function, insert.
self.values.insert(index, value)
def contains(self, value):
index = self.binary_search(value, self.values, 0, len(self.values))
return index < len(self.values) and value == self.values[index]Insertion with sorted list algorithm has big-O of O(log2n)+O(n), which rounds to O(n). This would be when the inserting needs to occur at the first of the list, and all the items in the list are scooted to the right. The big-O of containment check is O(log2(n)).
Unsorted List Set
The code for unsorted list is simple. When the UnsortedListSet
is initialized, it creates an empty list:
class UnsortedListSet(object):
def __init__(self):
self.values = []
For insert and contains, the algorithm checks one
number at a time from index of zero to the end of the list:
def insert(self, value):
if not self.contains(value):
self.values.append(value)
def contains(self, value):
for x in self.values:
if x == value:
return True
return False
The big-O of insert and contains for
UnsortedListSet are both O(n).
Visualizing Performance
I collected 100 data points of each set implementation. I used R and ggplot2 for visualizing the data. The plot of the data on a log2 x-scale and y-scale looks like below:

While it appears that I collected each operation data at a different n-sizes, each group of four boxes actually belongs to one n-size. ggplot2 automatically spreads the box plots so that it's easier to see the individual boxes. I used box plot because it accentuates the subtle differences between operations with random and non-random ordered numbers, rather than overlapping them like a point plot would. Let's dive into the data a little more, and look at insertion and containment check separately.
Containment Check: non-random and random
In the above plot in the UnsortedListSet plot, you can see
that there are two extreme outliers that took about 27 times
longer for completing the contains operation. It is
odd that only two points are much slower than the other data
points. I think it could have been either the order of the
queries tested the worst case performance, or something
interrupted the operations somehow. When sorted in decreasing
order, you can see that these outliers are quite large
compared to the third largest value.

Either way, I decided to exclude the two outliers so that plots look cleaner. I wouldn't recommend completely excluding outliers usually, but in this case, there are only 2 points so I removed them from the data.
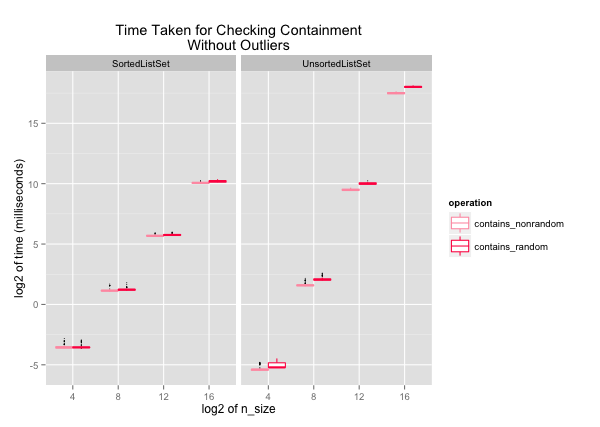
The big-O of containment-check would be O(log2(n))
for SortedListSet, and O(n)
for UnsortedListSet.
It is clear that the time taken for contains in
SortedListSets increases at a slower rate than in
UnsortedListSets, as expected. It is interesting that the
SortedListSet starts to significantly outperform
UnsortedListSet at n > 28. More
interestingly, SortedListSet is in fact slower
than UnsortedListSet when n-size is small. The
overhead cost of sorting via binary search must be larger than
the benefit of checking containment in a sorted list.
The difference between checking containment of numbers in
non-random and random orders into a SortedListSet
almost does not exist. This is probably because every time a
new number is added to the sorted list, the algorithm does
binary search to find the correct index for the number. For
a SortedListSet, whether the input numbers are in
random or non-random order does not make a difference in the
resulting list.
This, however, is not true for a UnsortedListSet. If the input
numbers are given in a random order, the resulting list will
have numbers in a random order. contains in a
randomly ordered list takes longer than in an ordered list, as
you can see in the plot.
Insertion: non-random and random
The big-O of insertion would be O(log2n + n), which
rounds to O(n) for SortedListSet. This is the sum
of bineary search
and Python's
built-in insert
operation. For UnsortedListSet, the big-O of
insertion is O(n).
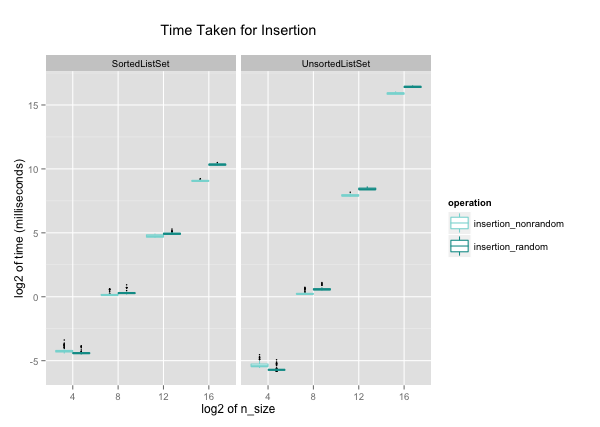
Like in contains, the time it takes to insert numbers
increases at a slower rate in SortedListSet. Again,
SortedListSet actually takes longer insertion time for n < 28,
and starts to outperform UnsortedListSet for n > 28.
Unlike contains, the difference between inserting
numbers in random and non-random orders into
a SortedListSet exists. This is because when
inserting numbers in order, insertion is more like
Python's append, because the new number is always
added to the last of the list. In other words, none of the
items in the list is moved, and its big-O is O(1). This is
much smaller than when the inserting numbers in random order,
which will have big-O of O(n). Meanwhile, insertion
in UnsortedListSet follows a similar trend as
its contains.
One thing I cannot explain about insertion is how inserting randomly ordered numbers take shorter time than ordered numbers at n = 24. It very well could be noise in data, or an interesting trend.
Conclusion and Closing Thoughts
I wanted to compare the real world performace to theoretical big-O
in the plots, but I had difficult time representing the big-O. For
example, I understand that insertion for UnsortedListSet is O(n) but
that doesn't mean it should be plotted as y = x. What would be the
coefficient? What about the intercept?
I'm also looking forward to implementing and visualizing
TreeSets. I wrote a script for
a UnbalancedTreeSet, but for n > 28,
it would reach the recursion limit and crash. Currently, the
algorithm is implemented recursively, and I'm thinking about
how to do it iteratively.